What is Parent Function & How to Find It?

As you work with functions and their graphs, you’ll notice that most functions’ graphs follow similar patterns. This is because functions with the same degree will have similar curves and share the same parent functions.

A parent function represents the simplest form of a family of functions.

This definition perfectly summarizes what parent functions are. When graphing functions that are found in the same family, we use parent functions to guide us. In this article, we will:

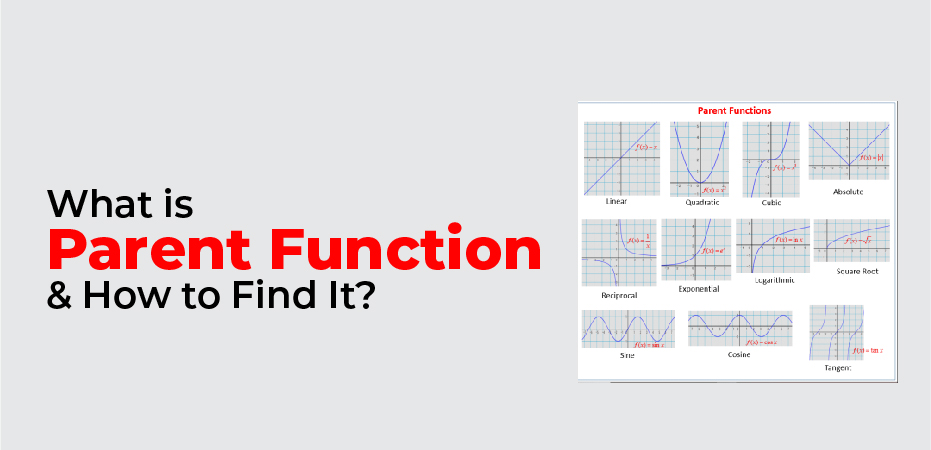
• Examine all the unique parent functions (you may have already encountered some).
• Identify the parent function to which a function belongs.

Identifying and graphing functions using their parent functions can help us understand them better, so what are we waiting for?

What is a Parent Function?

As we understand how important it is for us to master the different types of parent functions, let’s first take a look at what parent functions actually are. We will also look at how their families of functions are affected by their properties.

Parent function definition

Parents are the simplest form of a given family of functions. In mathematics, a family of functions is a group of functions with the same degree and, consequently, the same graph shape.

Four graphs display the U-shaped graph we call a parabola. The fact that they all share the same highest degree of two and the same shape allows us to group them as one family of functions. To which family do you think they belong?

All four are quadratic functions, and their simplest form would be y = x². Therefore, the parent function for this family is y = x².

Since parent functions are the simplest form of a given group of functions, they can immediately give you an idea of what a given function from the same family would look like.

How to Find the Parent Function?

How would we identify a function’s parent function if we were given a function or its graph? By remembering each function’s important properties, we can identify which of the parent graphs we’ve discussed matches the given graph.

The following are some guide questions that may be helpful:

• What is the function’s highest degree?
• Does it have a square root or cube root?
• Does the function appear at the exponent or denominator?
• Is the function’s graph decreasing or increasing?
• What is the function’s domain or range?

Inspecting some of these questions will allow us to deduce our options and eventually identify the parent function.

Let’s try f(x) = 5(x – 1)². f(x) has the highest degree of 2, so we know that it is a quadratic function. Therefore, its parent function is y = x².

Why not graph f(x) and confirm our answer as well?

It forms a parabola, indicating that its parent function is y = x².

Review the first few sections of this article and your notes, then let’s try out some questions to learn more about parent functions.

FAQs

Q: What are the 8 types of functions?

A: There are eight types: linear, power, quadratic, polynomial, rational, exponential, logarithmic, and sinusoidal.

Q: What are parent functions in algebra?

A: The simplest function that meets the definition of a certain type of function is called a parent function. The parent function of a family of linear functions is y = x. This is the simplest linear function.

Q: What are the five basic parent functions?

A: The basic functions include rational functions, exponential functions, basic polynomials, absolute values, and the square root function.

Q: What is a child’s function?

A; The child’s general behavior, emotions, temperament, and physical capacity fall under this domain.

Q: What is the transformation of a parent’s function?

A: With a parent function y=f(x) and its graph, certain modifications will result in easily observable changes in the graph. Changing f(x) to f(x−b) results in the graph being shifted b units to the right.

Q: What are four examples of functions?

A: We might define a function where the domain X is again a set of people, but the codomain is a set of numbers. For example, let Y be the set of whole numbers and define c so that for any person x, c(x) is the number of children of that person.