Do you need to find the volume of a rectangular pyramid? Whether you are a student studying geometry or an engineer working on a project, calculating the volume of a rectangular pyramid can be a crucial part of your work. A rectangular pyramid has a unique shape that requires a specific formula to calculate its volume.
This guide will walk you through the steps to find the volume of a rectangular pyramid, so you can confidently solve any problem that comes your way.
Before diving into the formula, it is important to understand the concept of a rectangular pyramid. This three-dimensional shape has a rectangular base and four triangular sides that meet at a point called the apex.
The properties of a rectangular pyramid differ from those of other pyramids, such as square or triangular pyramids, so it is essential to know what makes this shape unique. Once you have a solid understanding of the rectangular pyramid’s definition and properties, you can move on to calculating its volume.
Understanding the Concept of a Rectangular Pyramid
To properly grasp the concept of a rectangular pyramid, it’s crucial to understand its distinct characteristics.
A rectangular pyramid is a solid figure that has a rectangular base and four triangular faces that meet at a single point called the apex.
The base of the pyramid is a rectangle, which means that it has four sides and four right angles.
The triangular faces of the pyramid are isosceles triangles, which means that they have two equal sides and two equal angles.
One of the most important characteristics of a rectangular pyramid is its height. The height of a pyramid is the distance from the apex to the base, measured along a perpendicular line.
The height of a rectangular pyramid is important because it determines the length of the slant height, which is the distance from the apex to any point on the edge of the base.
The slant height is used to calculate the surface area and volume of the pyramid.
Understanding these basic characteristics of a rectangular pyramid is essential to finding its volume.
Definition and Properties of a Rectangular Pyramid
You might be interested to know that a rectangular pyramid is a three-dimensional figure with a rectangular base and triangular faces that meet at a common vertex. This means that the pyramid has four triangular faces and one rectangular face. The triangular faces are called lateral faces, while the rectangular face is the base of the pyramid. The common vertex where all the faces meet is called the apex of the pyramid.
One important property of a rectangular pyramid is that all the lateral faces are congruent. This means that they have the same shape and size. Additionally, the lateral faces are always isosceles triangles, which means that they have two sides of equal length.
Another property of a rectangular pyramid is that it has an altitude, which is the perpendicular distance from the apex to the base. This altitude is also the height of the pyramid. Knowing these properties is essential when finding the volume of a rectangular pyramid.
Formula for Calculating the Volume of a Rectangular Pyramid
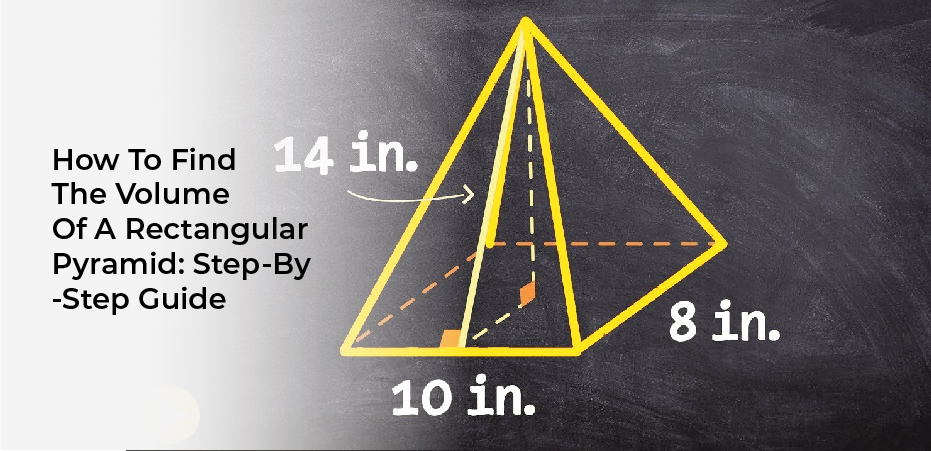
Get ready to learn how to calculate the volume of a rectangular pyramid using a simple formula! The formula for finding the volume of a rectangular pyramid is V = 1/3 Bh, where B is the area of the base and h is the height of the pyramid.
To find the area of the base, you simply multiply the length and width of the rectangle. Once you have the area of the base, you can plug it into the formula along with the height of the pyramid to find the volume.
It’s important to note that the height of the pyramid is not the same as the height of the rectangle. The height of the pyramid is the perpendicular distance from the base to the apex (the pointy top of the pyramid).
Additionally, when using the formula, make sure you are using the same units of measurement for all the values. With this simple formula, you can easily find the volume of a rectangular pyramid and apply it to various real-life scenarios.
Step-by-Step Guide to Finding the Volume
Ready for a quick and easy way to calculate the volume of a rectangular pyramid? Here’s a step-by-step guide to help you out.
First, measure the length, width, and height of the rectangular pyramid. The length and width should be the dimensions of the rectangular base, while the height should be the distance between the base and the peak.
Once you have these measurements, multiply the length, width, and height together. Then, divide the result by three. The final number is the volume of the rectangular pyramid. It’s that simple!
Just remember to use the correct units for your measurements. For example, if you measured the length, width, and height in inches, then your final volume will be in cubic inches. If you measured in meters, then your volume will be in cubic meters.
With this step-by-step guide, you’ll be able to find the volume of a rectangular pyramid with ease.
Real-World Examples and Applications of Rectangular Pyramid Volume
Nowadays, architects and engineers often use the volume of rectangular pyramids in designing buildings and structures. For example, the Louvre Pyramid in Paris is a famous example of a rectangular pyramid. The pyramid was designed by architect I.M. Pei and was completed in 1989. The pyramid has a base length of 35 meters and a height of 21.6 meters, making it a rectangular pyramid.
Knowing the volume of the pyramid was crucial in designing the structure and ensuring that it could withstand the weight of the glass panes and visitors.
Another example of a real-world application of rectangular pyramid volume is in the design of food packaging. Some brands of chocolate and other confectionery products use pyramid-shaped packaging. The pyramid shape not only makes the product stand out on shelves, but it also provides a unique way to package the product.
The volume of the pyramid-shaped packaging can be calculated to determine the amount of product that can fit inside. This is important for manufacturers to know how much of their product they can produce and sell in each packaging.
Overall, the volume of rectangular pyramids is a crucial measurement in designing structures and products in various industries.
Frequently Asked Questions
What is the difference between a rectangular pyramid and a square pyramid?
A rectangular pyramid has a rectangular base while a square pyramid has a square base. The number of faces and vertices in both pyramids differ. The volume of a rectangular pyramid is calculated using its base and height.
How do you determine the height of a rectangular pyramid if it is not given in the problem?
If the height of a rectangular pyramid is not given in the problem, you can use the Pythagorean theorem to calculate it. Measure the length and width of the base, and the slant height, and solve for the height using the formula h = sqrt(l^2 + w^2 – s^2).
Is there any other way to calculate the volume of a rectangular pyramid besides using the formula?
No, there isn’t another way to calculate the volume of a rectangular pyramid besides using the formula. You need the length, width, and height measurements to find the volume, so the formula is necessary.
Can the formula for calculating the volume of a rectangular pyramid be applied to other types of pyramids?
Yes, the formula for calculating the volume of a rectangular pyramid can be applied to other types of pyramids as long as the base is a rectangle. Simply substitute the appropriate measurements into the formula.
How does finding the volume of a rectangular pyramid relate to real-world applications, such as architecture or engineering?
When architects and engineers design buildings and structures, they often use rectangular pyramids to create unique shapes. Finding the volume of these pyramids is important for determining size, materials needed, and overall stability.
Conclusion
Congratulations! You’ve successfully learned how to find the volume of a rectangular pyramid.
Remember, a rectangular pyramid is a three-dimensional figure with a rectangular base and four triangular faces that meet at a common vertex. To find its volume, you need to use the formula V = (1/3)Bh, where B is the area of the base and h is the height of the pyramid.
By following the step-by-step guide provided, you can now confidently calculate the volume of any rectangular pyramid you encounter.
This skill can come in handy in various real-world scenarios, such as calculating the amount of material needed to fill a rectangular pyramid-shaped container or determining the volume of a building with a pyramid-shaped roof.
Keep practicing and applying this knowledge to become a pro at finding the volume of rectangular pyramids!