Imagine a scenario where you are analyzing the curve of a profit function to determine the most profitable production quantity. As you calculate the second derivative and look for points of inflection, you realize the critical role these points play in understanding the behavior of the function.
But how exactly do these inflection points impact decision-making processes and the overall shape of a graph? Stay tuned to explore the intricacies of finding points of inflection and their significance in mathematical analysis.
Definition of Points of Inflection
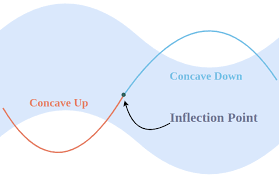
When analyzing functions, points of inflection are identified as locations where the concavity of the graph changes. These points mark transitions in the shape of the curve, indicating shifts from being concave upwards to concave downwards, or vice versa. At these inflection points, the curvature of the graph becomes flattened before changing direction.
To visualize this concept, imagine a rollercoaster ride. As the rollercoaster moves along the track, there are points where it smoothly transitions from going up to going down, or from turning left to turning right. These transition points are like the points of inflection in a mathematical function – they signal a change in the behavior of the curve.
Identifying points of inflection is crucial in understanding the behavior of a function. By recognizing where the concavity changes, you can gain insights into the overall shape and trends of the graph. Keep in mind that not all points where the curvature changes are inflection points; additional criteria need to be considered for accurate identification.
Criteria for Identifying Inflection Points
To identify inflection points in a function, observe where the concavity changes along the graph. An inflection point occurs where the concavity changes from being either concave up to concave down or vice versa. Mathematically, this change in concavity happens at points where the second derivative of the function equals zero or is undefined.
When analyzing a function, look for points where the second derivative changes signs. At these points, the concavity transitions, indicating a potential inflection point. Additionally, remember that not all points where the second derivative is zero are inflection points; they could be points of local maxima or minima instead. Therefore, it’s crucial to check the concavity on both sides of these points to confirm if they’re inflection points.
Techniques for Locating Inflection Points
When seeking to locate inflection points in a function, a common technique involves analyzing the sign changes of the second derivative. Inflection points occur where the concavity of a function changes, transitioning between being concave up and concave down. By examining the second derivative, you can determine where these changes in concavity happen.
To locate inflection points, follow these steps: first, find the second derivative of the function. Next, set the second derivative equal to zero to identify possible points of inflection. Then, determine the sign of the second derivative on either side of these points. If the sign changes from positive to negative or vice versa, you have found an inflection point.
Remember that not every point where the second derivative is zero corresponds to an inflection point. Additional analysis is necessary to confirm the nature of these critical points. By employing these techniques, you can effectively pinpoint the inflection points of a function with precision.
Analyzing Concavity Changes in Functions
Concavity changes in functions can be understood by examining the behavior of the second derivative. When the second derivative is positive, the function is concave up, forming a ‘smile’ shape. This indicates that the function is bending upwards.
Conversely, if the second derivative is negative, the function is concave down, creating a ‘frown’ shape, and the function is bending downwards. To analyze concavity changes, look for points where the second derivative changes sign. These points are potential inflection points where the concavity transitions from up to down or vice versa.
It’s important to note that the second derivative being zero at a point doesn’t guarantee an inflection point; further analysis is needed. By identifying these changes in concavity, you can gain insights into the behavior of the function and its curvature.
Understanding concavity changes helps in sketching accurate graphs and interpreting the behavior of functions.
Role of Inflection Points in Graphs
Inflection points play a crucial role in shaping the overall behavior of graphs. These points mark where the concavity of a function changes, indicating shifts from convex to concave or vice versa. Visually, inflection points appear as points where the curve transitions from bending one way to bending the other. They’re pivotal in understanding the curvature of a graph and can provide valuable insights into the function’s behavior.
When analyzing a graph, identifying inflection points helps in determining the overall shape of the curve. They serve as indicators of where the function transitions from being concave up to concave down or vice versa. By pinpointing these critical points, you can better comprehend how the function is behaving in different regions. Understanding the role of inflection points in graphs allows you to interpret the changing rates of increase or decrease more effectively, aiding in making informed decisions based on the function’s behavior.
Practical Applications of Inflection Points
Discover how inflection points play a crucial role in real-world scenarios, shaping decisions and outcomes based on the behavior of functions.
In fields like economics, inflection points are vital for determining trends in markets. By identifying where a curve transitions from concave to convex or vice versa, businesses can adjust strategies to capitalize on changing conditions. For instance, recognizing an inflection point in sales data could prompt a company to modify pricing or marketing techniques to boost revenue.
In engineering, inflection points help predict structural stability. Understanding where a beam’s curvature changes can prevent collapses and ensure the safety of buildings and bridges.
Moreover, in biology, inflection points assist in modeling population growth and disease spread accurately. By pinpointing where growth rates shift, scientists can develop more effective intervention strategies.
Importance of Inflection Points in Calculus
When dealing with inflection points in calculus, you’ll notice their crucial role in understanding the behavior of functions.
By analyzing sign changes at inflection points, you gain valuable insights into the concavity of a curve.
These points offer a graphical interpretation that aids in visualizing the changes occurring within a function.
Calculus and Inflection
Exploring the significance of inflection points in calculus sheds light on the behavior of functions at critical junctures. These points mark where the curvature of a function changes, indicating shifts from concave to convex or vice versa.
Understanding inflection points is crucial in calculus as they can help identify changes in the rate of growth or decline of a function. By analyzing inflection points, you can determine where a function transitions from being concave up to concave down, providing insights into the overall shape and behavior of the function.
Calculus relies on inflection points to pinpoint where functions exhibit changes in their concavity, making them a fundamental aspect of mathematical analysis.
Sign Change Analysis
Understanding the significance of inflection points in calculus is essential for analyzing changes in the behavior and curvature of functions. When you perform a sign change analysis around an inflection point, you gain insights into how the function’s concavity transitions.
By examining the intervals where the function’s second derivative changes sign, you can pinpoint where the inflection points lie. These points mark where the curvature of the function shifts from convex to concave, or vice versa. Identifying these critical points allows you to understand the function’s overall shape better and predict its behavior more accurately.
Sign change analysis provides a straightforward method to locate inflection points and grasp the underlying changes in a function’s concavity.
Graphical Interpretation Insights
To gain deeper insights into the behavior of functions, focus on the graphical interpretation of inflection points in calculus. Inflection points mark where the curvature of a function changes, transitioning between concave up and concave down.
By analyzing inflection points graphically, you can understand how the function’s rate of change is evolving. These points are critical as they can signify shifts in trends or behaviors within the function.
Visually, inflection points appear as points where the function’s curve changes its shape. This visual representation can offer intuitive understanding, aiding in predictions about the function’s behavior.
Identifying and interpreting inflection points graphically allows you to grasp the function’s overall trend and anticipate significant changes in its behavior.
Frequently Asked Questions
Yes, points of inflection can occur in functions with discontinuities or sharp corners. These points mark where the concavity changes, regardless of abrupt changes in the function. They are crucial for analyzing curves.
When looking at a graph, inflection points indicate where the curve changes concavity. Upward-facing curves shift from concave down to concave up at these points, while downward-facing curves transition from concave up to concave down.
Yes, inflection points are always associated with changes in concavity. They mark where a curve transitions from being concave up to concave down or vice versa. Identifying these points helps understand the graph’s behavior.
Conclusion
You now understand how to find points of inflection in mathematical analysis. By identifying these critical points where concavity changes, you can gain insights into the behavior of functions and graphs.
Remember to use the criteria and techniques discussed to locate inflection points accurately. Keep practicing to sharpen your calculus skills and apply this knowledge to solve real-world problems effectively.
Good job on mastering the concept of inflection points!