In some cases the graphs appear similar, but they may have different widths – and this is something that you may have already experienced. This might be because they may have been stretched horizontally by extending their base function. There are a number of techniques for writing functions graphs, but one of the most popular ones is horizontal stretching. Therefore, understanding how this technique works before applying it is a very important step.
If a chart is expanded vertically, it’s because the x-axis is raised and the y-axis is shifted. Getting a sense of how graphs can be stretched horizontally will be useful if we are looking to graph a family of functions. Additionally, we can learn how to plot as well as refine a new function more precisely and quickly based upon the scaling factors that we apply.
You should ensure that you have thoroughly reviewed your understanding of parent functions, translations, and vertical stretches if you would like to move on to the next section.
- It is important in our study of Python to understand the different kinds of parent functions that we may encounter on our way.
- In particular, you should refresh your knowledge of vertical transformations and horizontal transformations.
- It is important to know how they work in the simplest terms possible.
I have linked some articles on this page that may be helpful to you if you are in need of some refresher material. Now that we know the basics of horizontal stretching, let’s move onto exploring more about it when you’re ready.
Horizontal Stretch: What Is It?
In order to stretch a function horizontally, multiply the input values by the scaling factor, a, where 0 < 1/a < 1 are your input values. Can you explain what this means for functions such as f(x)? A scale factor of 1/a multiplied by x will stretch f(x)’s graph horizontally by a factor of a.
Let’s take a look at how f(x) = x2 will get affected by the values of 1/2 and 1/3.
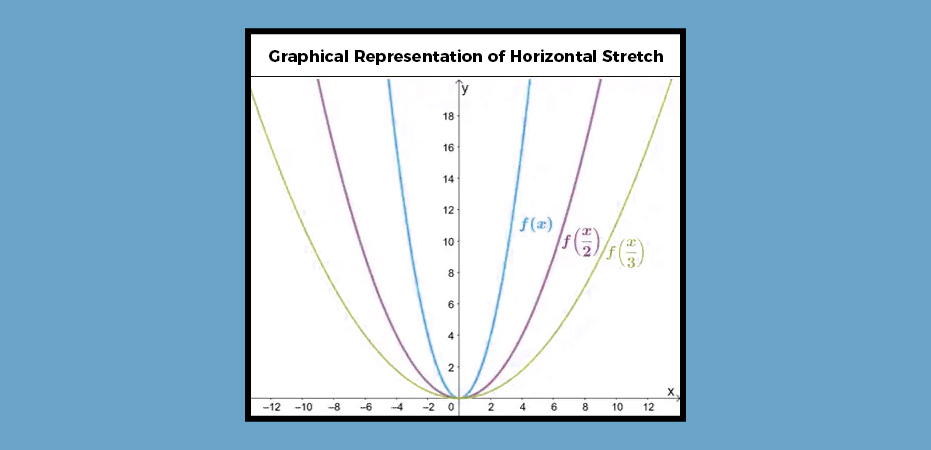
I was surprised to see that, as expected, the graph stretched by a factor of two to three by a factor of two to three. However, what you might have observed is how the y values remained the same.
I have noticed this to be the case for all vertical stretches. The only time a graph is horizontally stretched away from the y axis is when the graph stretches away from the axes.
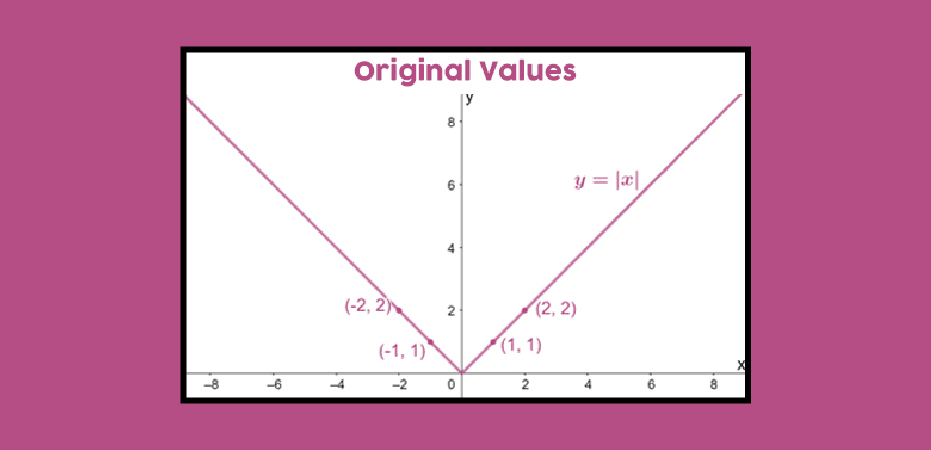
Horizontal stretch will exhibit similar properties on other functions. For example, we have f(x) = |x|, if we horizontally stretch this function’s graph to get g(x), the new expression of the function can be written as |1/3 ∙ x| = |x/3|.
Let us compare some values:
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) = |x| | 2 | 1 | 0 | 1 | 2 |
If we increase all x-coordinates 3 times, the output values will still remain the same for all of the x values.
| x | -6 | -3 | 0 | 3 | 6 |
| g(x) = |x/3| | 2 | 1 | 0 | 1 | 2 |
What Are The Steps For Horizontally Stretching A Function?
The previous section discussed horizontal stretches and their effects on the base function, and now it is time to apply these concepts to graphs of functions. There are a few tricks you can apply to stretch graphs horizontally as quickly as possible:
- The y-coordinates must stay the same while the graph is stretched horizontally.
- Due to the same y-coordinates, the y-intercept remains the same.
- Make sure that you double-check crucial points on the graph, including intercepts and maximum points.
- Be sure to scale the coordinates correctly as well.
Let’s visualize the effects of a horizontal stretch on a graph by mapping y = x and y = x/3 by using the table of values shown in the previous section.
We expect the graphs to extend along the base while the y values remain constant, as we discussed earlier.
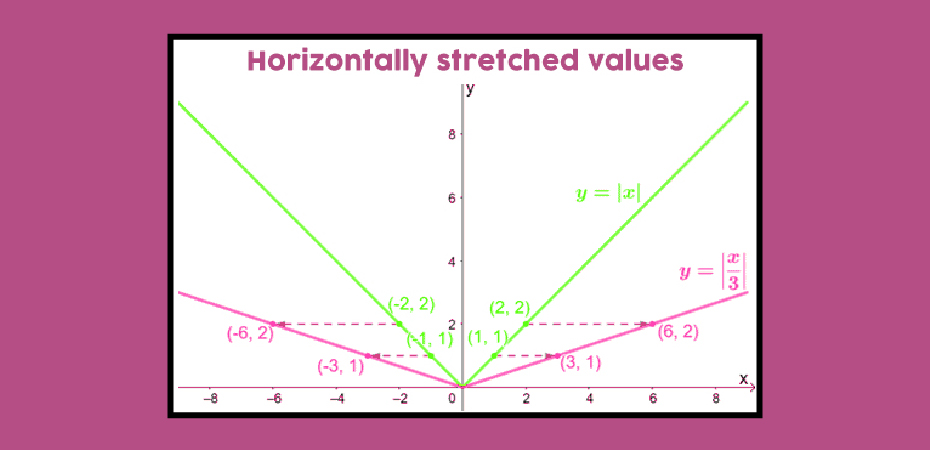
The parent function of y = x by 3 times makes y = x/3. Using the same process to horizontally stretch the graphs of other functions, we can confirm this point.
Interested in graphing more functions and extending horizontally? First, let’s review what we have learned so far.
Overview Of Horizontal Stretch Definitions And Properties
When answering problems involving horizontal stretches and graphing functions, remember the following important points:
- If we also increase the input value by a, we can horizontally stretch a graph by 1/a.
- The x coordinates of f(x) are multiplied by a when f(ax) is stretched horizontally.
- The y-intercepts are preserved.
- This result will have the same range, but a different domain.
- Taking a point (m, n) and stretching it horizontally, it becomes (am, n).
Always look back to these five-point shots when in doubt. It can be extremely useful to be able to master the technique of horizontally stretching graphs so that we can graph function behavior more quickly.


