A Calculus Basics

In this article, you’ll learn how to estimate the derivative from a table. Calculus may seem intimidating, but understanding derivatives is essential. Estimating derivatives allows you to gather data and interpret it effectively. By using difference quotients or average rates of change, you can estimate the derivative accurately.

However, it’s important to be aware of the limitations of estimating derivatives from a table.

Stay tuned to discover the practical applications of estimating derivatives in various fields.

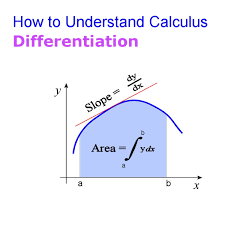
What Is Calculus

Calculus is a branch of mathematics that deals with the study of change using rates and quantities. It’s a powerful tool that allows you to understand and analyze complex systems.

With calculus, you can find the slope of a curve at any given point, which helps you understand how things are changing. This is especially useful in physics, engineering, and economics, where rates of change are crucial.

Calculus also helps you find the area under a curve, which is valuable in solving real-world problems involving volume, distance, and accumulation.

Understanding Derivatives

Let’s start by understanding the purpose of derivatives.

Derivatives allow us to calculate instantaneous rates of change, which can help us analyze the behavior of a function at any given point.

By estimating derivatives, we can determine how quickly a quantity is changing at a specific moment.

This concept has practical applications in various fields like physics, economics, and engineering.

Purpose of Derivatives

To truly understand derivatives, you should frequently observe how they provide insights into the rate of change of a function. The purpose of derivatives is to help us analyze and understand the behavior of functions at specific points.

By calculating the derivative of a function, we can determine the slope of the tangent line at any given point on the graph. This information allows us to identify where the function is increasing or decreasing, locate maximum and minimum points, and predict the behavior of the function in different scenarios.

Derivatives also help us solve optimization problems by finding the maximum or minimum values of a function within a given domain. Furthermore, derivatives are essential in physics and engineering, where they’re used to describe the rate of change of physical quantities such as velocity and acceleration.

Calculating Instantaneous Rates

To calculate instantaneous rates, you need to understand how derivatives represent the rate of change of a function at a specific point. Derivatives provide valuable information about the behavior of a function, allowing us to determine how it’s changing at any given moment.

By finding the derivative of a function, you can determine the slope of the tangent line to the graph at a particular point. This slope represents the instantaneous rate of change of the function at that point.

To calculate this rate, you can use a variety of methods, such as the limit definition of the derivative or the power rule. These techniques allow you to find the derivative and determine the precise rate of change at any specific point on the graph.

Practical Applications of Derivatives

To understand derivatives better, you can explore the practical applications of these important mathematical tools.

Derivatives aren’t just abstract concepts; they’ve real-world applications that can help you solve problems in various fields.

For example, in physics, derivatives can be used to calculate velocity and acceleration of moving objects.

In economics, derivatives are used to analyze and predict changes in variables like cost, revenue, and profit.

In engineering, derivatives are used to determine rates of change in physical quantities, such as the slope of a curve or the rate at which a system is changing.

Understanding derivatives can also be useful in fields like biology, chemistry, and computer science.

Importance of Estimating Derivatives

When it comes to estimating derivatives, there are many practical applications that make it an important skill to develop. By being able to estimate derivatives, you can make predictions about the behavior of a function in real-world scenarios, such as predicting the velocity of an object or the rate of change in a business.

Additionally, estimating derivatives enhances your problem-solving abilities in mathematics, allowing you to tackle more complex problems with ease.

Practical Applications of Estimation

Estimating derivatives is essential for understanding real-world applications and making accurate predictions. By estimating the derivative, you can determine the rate of change of a function at a specific point.

This information is crucial in various fields such as physics, economics, and engineering. For example, in physics, estimating the derivative allows you to calculate the velocity of an object at a given time or determine the rate of change of temperature in a system.

In economics, estimating derivatives helps analyze supply and demand curves, allowing businesses to optimize production and pricing strategies.

In engineering, estimating derivatives helps in designing efficient systems, such as determining the rate at which a chemical reaction occurs in a chemical plant.

Estimating derivatives empowers you to make informed decisions and solve real-world problems effectively.

Enhancing Mathematical Problem-Solving

By estimating derivatives, you can enhance your mathematical problem-solving skills and effectively analyze real-world applications in various fields such as physics, economics, and engineering.

Estimating derivatives allows you to approximate the rate of change of a function at a specific point without needing to know the exact formula. This skill is valuable because in many real-world scenarios, the exact formula may not be readily available or may be too complex to work with.

By estimating derivatives, you can make quick and informed decisions, solve optimization problems, and understand the behavior of functions in different situations. It also enables you to make predictions and understand how small changes in variables can affect the overall outcome.

Gathering Data for Estimation

To gather data for estimation, you’ll need to determine the values of the function at specific points. This involves selecting several x-values within a given range and finding the corresponding y-values. To do this, you can refer to a table or a graph of the function. Simply choose different x-values and use the function to calculate the corresponding y-values.

It’s important to select a range of x-values that are evenly spaced to ensure accurate estimation. Once you have gathered the necessary data points, you can use them to estimate the derivative of the function at a particular point. By calculating the average rate of change between adjacent points, you can obtain a rough estimate of the derivative.

Interpreting a Table of Values

When interpreting a table of values, you can analyze the gathered data to understand the relationship between the x-values and their corresponding y-values, continuing the discussion on gathering data for estimation.

By examining the values in the table, you can identify patterns and trends. Look for any consistent changes in the y-values as the x-values increase or decrease. This will give you insight into how the function is behaving.

Additionally, pay attention to any outliers or anomalies in the data that may indicate unusual behavior. By carefully interpreting the table, you can gain a better understanding of the function and make more accurate estimations.

Remember to consider the precision of the values and any limitations in the data collection process.

Method 1: Using Difference Quotients

To estimate the derivative from a table, you can use a method called Difference Quotients, which involves calculating the rate of change between two points on the table. This method is useful when you have a set of data points and want to approximate the slope of the curve at a specific point.

To use Difference Quotients, you select two points on the table that are close to the desired point. Then, you find the difference in the y-values and divide it by the difference in the x-values of the two points. This gives you an approximation of the slope or rate of change at that point.

Method 2: Using Average Rates of Change

To estimate the derivative from a table, you can also use the method of calculating average rates of change.

This method involves finding the average rate of change between two points on the table. To do this, you need to determine the difference in the y-values and the difference in the x-values of the two points. Then, divide the difference in the y-values by the difference in the x-values. This will give you the average rate of change between the two points.

The average rate of change represents an approximation of the derivative at a specific point on the table. By calculating the average rates of change for different pairs of points, you can estimate the derivative at various points on the table.

Limitations of Estimating Derivatives From a Table

Calculating the average rates of change to estimate the derivative from a table has its limitations. While this method can provide a rough estimate of the derivative at a specific point, it may not accurately capture the behavior of the function between data points. The accuracy of the estimate heavily depends on the spacing between the points on the table.

If the points are too far apart, the estimate may not reflect the true rate of change at any given point. Additionally, this method assumes that the function is linear between each pair of data points, which mightn’t be the case for all functions.

Therefore, it’s important to recognize the limitations of estimating derivatives from a table and to use more advanced techniques, such as calculus, when a more precise estimate is needed.

Applications of Estimating Derivatives

When estimating derivatives from a table, you can apply this technique to various real-world situations. By estimating the derivative, you can determine the rate of change of a quantity at a specific point.

This can be useful in fields such as physics, economics, and engineering. For example, in physics, estimating the derivative can help analyze the velocity of an object at a given time. In economics, it can be used to study the marginal cost or revenue of a business. In engineering, estimating derivatives can aid in understanding the rate at which a system changes over time, such as the speed of a machine.

Frequently Asked Questions

Can I Estimate the Derivative of Any Function Using a Table of Values?

Yes, you can estimate the derivative of any function using a table of values. By calculating the slope between consecutive points, you can approximate the rate of change and get an idea of the derivative.

How Accurate Are the Estimates Obtained From the Methods Described in the Article?

The estimates obtained from the methods described in the article are accurate to a certain extent. However, it is important to note that these estimates may not be as precise as those obtained through more advanced calculus techniques.

Can I Estimate Higher-Order Derivatives From a Table of Values?

Yes, you can estimate higher-order derivatives from a table of values. It involves using the same methods described in the article but applying them to the higher-order differences in the table.

Are There Any Alternative Methods to Estimate Derivatives From a Table?

Yes, there are alternative methods to estimate derivatives from a table. One option is using finite differences, where you calculate the difference between consecutive values to approximate the derivative.

What Are Some Real-Life Applications Where Estimating Derivatives From a Table Is Useful?

Some real-life applications where estimating derivatives from a table is useful include analyzing stock market trends, predicting population growth rates, and understanding the rate of change in physical processes like temperature or velocity.

Conclusion

In conclusion, estimating derivatives from a table is a valuable skill in calculus. By using methods such as difference quotients and average rates of change, we can approximate the rate at which a function is changing at a specific point.

While estimating derivatives from a table has its limitations, it’s still a useful tool in various applications. So, keep practicing and honing your skills in estimating derivatives to excel in calculus.